¿Buscas un software de matemáticas gratuito, potente y fácil de usar? Maxima es una de las mejores herramientas de cálculo simbólico y numérico que puedes encontrar hoy en día. Este programa de código abierto permite realizar operaciones matemáticas avanzadas como derivadas, integrales, álgebra lineal, resolución de ecuaciones diferenciales y gráficas en 2D y 3D, todo sin necesidad de pagar licencias costosas como las de Mathematica o Maple.
En este artículo descubrirás qué es Maxima, sus principales características, ventajas, desventajas y cómo empezar a usarlo para tus estudios, investigaciones o proyectos profesionales. Tanto si eres estudiante, profesor o investigador, aquí encontrarás una guía completa que te ayudará a aprovechar al máximo este poderoso sistema de álgebra computacional.
¿Qué es Maxima?
Maxima es un sistema de álgebra computacional (CAS, por sus siglas en inglés) diseñado para realizar cálculos matemáticos simbólicos y numéricos con una precisión sobresaliente. Se trata de un software de código abierto y totalmente gratuito, ideal para quienes necesitan resolver problemas matemáticos avanzados sin depender de costosas licencias comerciales.
Su origen se remonta al legendario Macsyma, un programa desarrollado en el MIT durante la década de 1960, considerado pionero en el campo del cálculo algebraico asistido por computadora. Maxima es el único descendiente directo de aquel proyecto que sigue activo, actualizado y disponible bajo la licencia GNU GPL, lo que garantiza su libertad de uso, distribución y modificación.
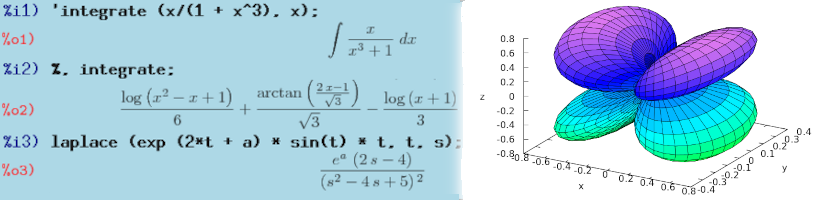
A lo largo de los años, Maxima ha evolucionado hasta convertirse en una herramienta completa y versátil. Permite trabajar con derivadas, integrales, álgebra lineal, ecuaciones diferenciales, series de Taylor, tensores y más, todo con gran exactitud. Además, integra gráficas en 2D y 3D, lo que facilita la visualización de funciones matemáticas y resultados complejos.
En cuanto a compatibilidad, Maxima es multiplataforma: puede instalarse en Windows, macOS y Linux, e incluso cuenta con versiones disponibles para Android, lo que lo hace accesible desde casi cualquier dispositivo. Gracias a su comunidad activa y a interfaces como wxMaxima, su uso resulta más sencillo e intuitivo, acercando el poder del álgebra computacional a estudiantes, docentes, investigadores y profesionales de diversas áreas.
Maxima combina la solidez de un legado histórico con la flexibilidad del software libre, posicionándose como una de las mejores alternativas a programas comerciales como Mathematica o Maple, pero con la gran ventaja de ser completamente gratuito.
¿Para qué sirve Maxima?
Maxima sirve como una herramienta informática para realizar cálculos matemáticos de manera precisa y eficiente. Su función principal es automatizar operaciones que serían largas, complejas o propensas a errores si se hicieran a mano, abarcando tanto el cálculo simbólico (manipulación de expresiones algebraicas exactas) como el cálculo numérico (aproximaciones y resultados con diferentes niveles de precisión).
En términos generales, Maxima se utiliza para:
- Resolver y simplificar expresiones matemáticas.
- Manipular ecuaciones y obtener resultados exactos o aproximados.
- Trabajar con matrices, vectores y tensores.
- Analizar funciones a través de derivadas, integrales y series.
- Generar representaciones gráficas en dos y tres dimensiones.
Gracias a estas capacidades, Maxima se convierte en un apoyo esencial para estudiantes, profesores, investigadores y profesionales que necesitan un entorno confiable para explorar, enseñar o aplicar conceptos matemáticos sin necesidad de recurrir a software propietario de alto costo.
Características principales de Maxima
Maxima es mucho más que una calculadora avanzada: se trata de un sistema de álgebra computacional completo, capaz de manejar operaciones simbólicas, numéricas y gráficas con gran exactitud. Sus características lo convierten en una herramienta flexible y poderosa, ideal tanto para el aprendizaje como para la investigación.
A continuación, te presentamos sus funciones más destacadas:
1. Cálculo simbólico
Maxima sobresale en la manipulación algebraica, ofreciendo resultados exactos sin aproximaciones innecesarias.
- Derivación e integración de funciones.
- Expansión de expresiones en series de Taylor.
- Resolución de ecuaciones diferenciales ordinarias.
- Simplificación y reestructuración de expresiones algebraicas complejas.
2. Cálculo numérico
Además del cálculo exacto, Maxima permite trabajar con aproximaciones numéricas de alta precisión.
- Soporte para enteros de precisión arbitraria.
- Cálculos con números de coma flotante y control de la precisión.
- Resolución de sistemas de ecuaciones lineales y no lineales con métodos eficientes.
3. Álgebra lineal y matrices
El álgebra lineal es otra de las áreas fuertes de Maxima.
- Operaciones con vectores y matrices (suma, producto, transposición, inversa, etc.).
- Cálculo de determinantes, autovalores y autovectores.
- Soporte para tensores, lo que amplía sus aplicaciones en física e ingeniería.
4. Visualización gráfica
Maxima facilita la interpretación de resultados a través de gráficos matemáticos.
- Generación de gráficas en 2D y 3D.
- Representación visual de funciones y datos numéricos.
- Integración con GNUplot para obtener visualizaciones de mayor calidad.
5. Extensibilidad y programación
Además de sus funciones integradas, Maxima es altamente personalizable y programable.
- Lenguaje propio con sintaxis tipo ALGOL y semántica basada en Lisp.
- Posibilidad de crear módulos adicionales en Lisp para ampliar sus capacidades.
- Generación automática de código en Fortran para cálculos de alto rendimiento.
6. Interfaces gráficas
Aunque Maxima puede ejecutarse en modo consola, existen interfaces que hacen su uso mucho más amigable:
- wxMaxima: interfaz estilo notebook, muy similar a Mathematica, ideal para trabajar con documentos interactivos.
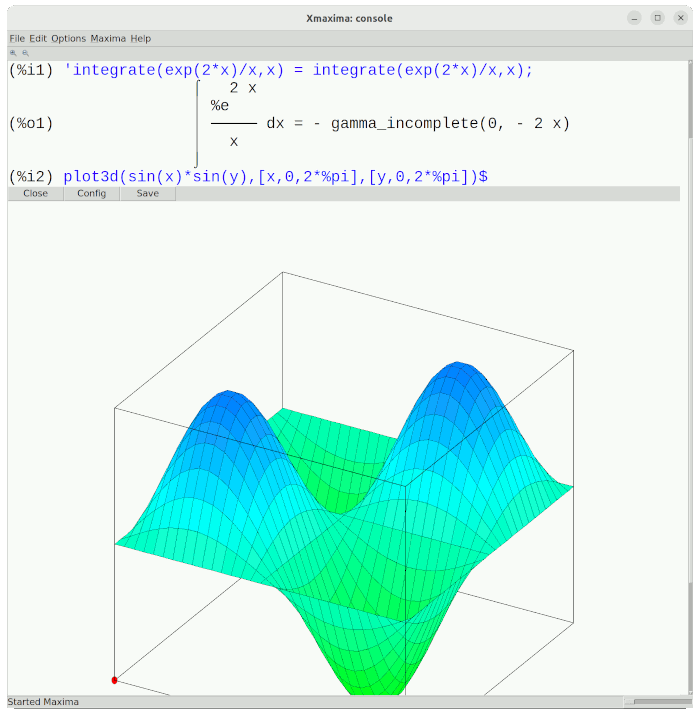
- Xmaxima: una interfaz ligera y sencilla para quienes buscan simplicidad.
- Integración con herramientas externas como TeXmacs, SageMath y Emacs, que enriquecen la experiencia de trabajo.
Las características de Maxima lo convierten en un software matemático completo y versátil, capaz de cubrir desde cálculos básicos hasta análisis avanzados en múltiples ramas de las matemáticas y las ciencias aplicadas.
Ventajas de usar Maxima
Elegir Maxima como herramienta matemática ofrece numerosos beneficios frente a otros programas comerciales. Su combinación de potencia, libertad y accesibilidad lo convierte en una opción ideal tanto en el ámbito académico como profesional. Estas son algunas de sus principales ventajas:
1. Gratis y de código abierto
Maxima es un software 100% libre y gratuito, distribuido bajo licencia GNU GPL. No necesitas pagar licencias costosas como ocurre con Mathematica o Maple. Además, al ser de código abierto, cualquier usuario o desarrollador puede estudiar su funcionamiento, adaptarlo y mejorarlo según sus necesidades.
2. Amplia comunidad y soporte
El proyecto cuenta con una comunidad activa de usuarios y desarrolladores que aporta documentación, foros de ayuda, listas de correo y tutoriales en línea. Gracias a esto, Maxima recibe actualizaciones frecuentes y nuevas funciones que lo mantienen vigente a pesar de sus décadas de existencia.
3. Precisión y potencia en los cálculos
Maxima está diseñado para manejar operaciones matemáticas de gran complejidad con un nivel de precisión sobresaliente. Es capaz de trabajar con enteros de precisión arbitraria, cálculos simbólicos exactos y operaciones numéricas controladas, lo que lo hace ideal para investigación científica y proyectos que requieren resultados confiables.
4. Multiplataforma y accesible
Se puede instalar en prácticamente cualquier sistema operativo: Windows, macOS, Linux e incluso Android. Esto garantiza que tanto estudiantes como profesionales puedan acceder a la herramienta desde diferentes dispositivos, sin limitaciones técnicas.
5. Integración flexible con otros entornos
Maxima no está aislado: se integra fácilmente con otras plataformas y programas matemáticos. Puede conectarse con TeXmacs, SageMath, Emacs y aprovechar interfaces gráficas como wxMaxima, lo que amplía sus posibilidades y lo convierte en un software adaptable a distintos flujos de trabajo.
👉 En conclusión, las ventajas de Maxima lo convierten en una alternativa poderosa y libre a los sistemas de álgebra computacional comerciales, ideal para quienes buscan un software robusto, versátil y accesible.
Desventajas de Maxima
- Curva de aprendizaje pronunciada: su sintaxis puede parecer poco intuitiva para principiantes.
- Interfaz menos moderna: aunque wxMaxima mejora mucho la experiencia, sigue siendo menos atractiva que la de Mathematica o Maple.
- Menos soporte comercial: al ser un proyecto comunitario, el soporte oficial es limitado frente a las grandes empresas.
Aplicaciones y casos de uso de Maxima
Gracias a su potencia y versatilidad, Maxima se utiliza en una amplia variedad de contextos académicos, científicos y profesionales. Su capacidad para combinar cálculo simbólico, numérico y visualización lo convierte en una herramienta indispensable en diferentes áreas del conocimiento.
A continuación, exploramos sus principales aplicaciones:
1. Educación
En el ámbito educativo, Maxima es un recurso muy valioso para estudiantes, docentes y centros académicos.
- Permite enseñar y aprender cálculo diferencial, integral, álgebra lineal, geometría y métodos numéricos de manera práctica.
- Facilita la creación de ejercicios interactivos y ejemplos visuales gracias a su integración con wxMaxima, que ofrece un entorno tipo notebook.
- Ayuda a los estudiantes a verificar resultados y comprender procesos matemáticos de forma más clara.
2. Investigación científica
En la investigación, Maxima es empleado por matemáticos, físicos e ingenieros para modelar problemas complejos.
- Resolución de ecuaciones diferenciales en física teórica y aplicada.
- Análisis de series, transformadas y sistemas dinámicos.
- Cálculos simbólicos de alta precisión en experimentos y simulaciones.
Su capacidad para manejar operaciones de gran complejidad lo convierte en una alternativa confiable frente a software comercial en proyectos científicos y académicos.
3. Ingeniería y desarrollo tecnológico
En el campo de la ingeniería, Maxima es útil para el análisis y diseño de sistemas.
- Simulación matemática de circuitos, estructuras y procesos físicos.
- Optimización y resolución de problemas de ingeniería.
- Modelado de sistemas lineales y no lineales, con aplicaciones en electrónica, mecánica y telecomunicaciones.
Gracias a su compatibilidad multiplataforma y su flexibilidad, Maxima puede integrarse en flujos de trabajo más amplios de análisis y desarrollo tecnológico.
4. Autoaprendizaje
Maxima también es muy popular entre autodidactas y entusiastas de las matemáticas.
- Ofrece un entorno libre y accesible para explorar conceptos avanzados sin necesidad de costosos programas.
- Permite a los usuarios practicar derivadas, integrales, matrices y gráficas de manera interactiva.
- Es una excelente herramienta de apoyo para quienes se preparan en áreas de ciencias, ingeniería o programación matemática.
✅ Las aplicaciones de Maxima abarcan desde la enseñanza básica hasta la investigación avanzada y el desarrollo tecnológico, lo que demuestra su enorme potencial como software de matemáticas libre y de código abierto.
Maxima vs. otros software matemáticos
Cuando se habla de software para cálculo simbólico y numérico, nombres como Mathematica, Maple o MATLAB suelen aparecer en primer lugar. Sin embargo, Maxima se posiciona como una alternativa sólida, gratuita y de código abierto, que ofrece muchas de las funciones esenciales de estos programas comerciales.
1. Maxima vs. Mathematica
- Costo: Mathematica requiere licencias costosas, mientras que Maxima es totalmente gratuito.
- Funcionalidad: Mathematica ofrece una integración más avanzada en áreas como inteligencia artificial, visualización 3D y análisis de datos. Maxima, en cambio, se centra en lo esencial: cálculo simbólico, algebraico y numérico.
- Accesibilidad: Maxima resulta ideal para estudiantes y profesores que no tienen acceso a software de pago, sin sacrificar precisión en los cálculos matemáticos.
2. Maxima vs. Maple
- Potencia: Maple es uno de los referentes en cálculos matemáticos avanzados, especialmente en cálculo simbólico y álgebra computacional.
- Ventaja de Maxima: Aunque no tiene todas las funciones gráficas y de interfaz de Maple, Maxima cumple muy bien con las operaciones simbólicas, diferenciales y algebraicas.
- Licenciamiento: Maple es software propietario, mientras que Maxima es libre y tiene una comunidad que asegura su constante evolución.
3. Maxima vs. MATLAB
- Enfoque: MATLAB está orientado principalmente al cálculo numérico, simulación y análisis de datos, siendo muy usado en ingeniería y ciencias aplicadas.
- Fortaleza de Maxima: Destaca en el cálculo simbólico (derivadas, integrales, álgebra) donde MATLAB necesita de un complemento adicional como el Symbolic Math Toolbox.
- Costo y accesibilidad: MATLAB requiere licencias de pago, lo que lo hace menos accesible frente a la gratuidad de Maxima.
4. Conclusión comparativa
- Si lo que necesitas es precisión en cálculo simbólico, accesibilidad y un entorno libre, Maxima es la mejor opción.
- Si buscas herramientas más integradas en big data, visualización avanzada o inteligencia artificial, programas comerciales como Mathematica o MATLAB pueden ser más adecuados, aunque a un alto costo.
En definitiva, Maxima se destaca como una alternativa eficiente, libre y práctica, especialmente en educación, autoaprendizaje e investigación, siendo el punto de entrada ideal al mundo del software matemático profesional.
Cómo aprender Maxima: Recursos y Guías Prácticas
Aprender a usar Maxima no tiene por qué ser complicado. Existen múltiples recursos gratuitos y accesibles que te ayudarán a dominar este potente sistema de álgebra computacional, desde manuales básicos hasta tutoriales avanzados.
1. Documentos y Manuales en Español
- «Primeros pasos en Maxima» – Manual introductorio en PDF por Mario Rodríguez Riotorto. Cubre instalación, primeros pasos, álgebra, gráficos, probabilidad, programación y más. Una guía esencial y completa en español. maxima.sourceforge.io
- Documentación oficial en español – Disponible en el sitio web del proyecto, incluye manuales de referencia, tutoriales y guías de uso maxima.sourceforge.io.
2. Documentación oficial
El primer paso para familiarizarte con Maxima es revisar su documentación:
- 📖 Manual oficial de Maxima (en inglés): guía completa de funciones, comandos y ejemplos.
- 📑 Introducción a Maxima en español (PDF): versión en español del manual, ideal para estudiantes y docentes.
3. Tutoriales en línea
Existen tutoriales creados por la comunidad que explican cómo usar Maxima paso a paso:
- 🌐 Maxima by Example (en inglés): colección extensa de ejemplos prácticos.
- 📘 Guía rápida de wxMaxima (interfaz gráfica de Maxima).
4. Cursos y videos en YouTube
Los videos son un recurso excelente para aprender de forma visual:
- ▶️ Curso básico de Maxima (YouTube): recopilación de tutoriales en español.
- ▶️ wxMaxima tutorial (YouTube): videos para aprender a trabajar con la interfaz gráfica.
5. Comunidades y foros
La comunidad de Maxima es muy activa y siempre dispuesta a ayudar:
- 💬 Foro oficial de SourceForge.
- 📢 Grupo de usuarios en Google Groups.
- 🌍 Stack Overflow (Maxima): espacio para resolver dudas técnicas.
6. Libros recomendados
Si prefieres aprender con un enfoque más estructurado, existen libros que cubren desde lo básico hasta lo avanzado:
- 📕 Maxima by Example – Richard H. Rand.
- 📕 Maxima Tutorial with Examples – William F. Trench (disponible en línea).
👉 Con estos recursos podrás avanzar desde los primeros pasos hasta aplicaciones avanzadas de Maxima en educación, investigación y desarrollo. La clave está en combinar la teoría de la documentación con la práctica mediante ejemplos y ejercicios reales.
