¿Te has preguntado alguna vez qué es el cálculo integral y para qué sirve en la vida real? Tal vez al escuchar esas palabras pienses en fórmulas complicadas, pero la verdad es que detrás del cálculo integral se esconde una de las herramientas más poderosas que tiene la humanidad para comprender el mundo.
Imagina poder calcular el área bajo una curva, el volumen de una figura irregular, la distancia recorrida por un objeto en movimiento o incluso el crecimiento de una población. Todo eso —y mucho más— es posible gracias al cálculo integral.
En este artículo quiero invitarte a descubrir conmigo los fundamentos de esta rama de las matemáticas, su historia, sus aplicaciones y los métodos que permiten resolver problemas que, a simple vista, parecen imposibles. Verás que no es un tema inalcanzable: con la explicación adecuada puede ser apasionante, útil y hasta inspirador.
Así que acompáñame en este recorrido, porque al final no solo entenderás qué es el cálculo integral, sino que también podrás apreciar cómo este conocimiento conecta las matemáticas con la vida cotidiana y con los grandes avances de la ciencia y la tecnología.
¿Qué es el Cálculo Integral?
Cuando hablamos de qué es el cálculo integral, nos referimos a una rama de las matemáticas que estudia cómo acumular y sumar cantidades infinitamente pequeñas para obtener un resultado total. En otras palabras, el cálculo integral nos ayuda a responder preguntas como:
- ¿Cuál es el área bajo una curva?
- ¿Qué volumen ocupa una figura irregular?
- ¿Cuál es la distancia total recorrida por un objeto en movimiento continuo?
La idea principal es que, si dividimos un problema en muchas partes diminutas y luego sumamos todas esas pequeñas contribuciones, podemos encontrar el valor total de manera precisa. Imagina que quieres calcular la cantidad de agua que contiene una botella con una forma irregular. Si intentaras medirla directamente sería complicado, pero si la cortaras en muchas rebanadas muy delgadas y midieras el volumen de cada una para luego sumarlos, obtendrías el volumen total. Esa es la esencia del cálculo integral: acumular lo infinitamente pequeño para comprender lo grande.

Existen dos tipos fundamentales de integrales:
- Integral indefinida
Representa la familia de funciones cuya derivada es la función original. Se expresa como: $$
\int f(x)\,dx = F(x) + C
$$ donde $F'(x) = f(x)$ y $C$ es la constante de integración. Ejemplo sencillo: $$
\int 2x\,dx = x^2 + C
$$ - Integral definida
Permite calcular un valor numérico exacto, como el área bajo una curva entre dos puntos. Se representa como: $$
\int_a^b f(x)\,dx
$$ donde $a$ y $b$ son los límites de integración. Ejemplo sencillo: $$
\int_0^2 x\,dx = \left[ \frac{x^2}{2} \right]_0^2 = 2
$$
En términos prácticos, la integral definida transforma una función en un número que representa acumulación: ya sea un área, una distancia, un volumen o cualquier cantidad que pueda sumarse de manera continua.
En conclusión, el cálculo integral es el puente entre lo infinitamente pequeño y lo infinitamente grande, una herramienta que nos permite cuantificar procesos que cambian constantemente.
¿Para qué sirve el Cálculo Integral?
El cálculo integral sirve para medir, acumular y comprender fenómenos que cambian de manera continua. Su utilidad radica en que nos permite calcular valores totales a partir de pequeños cambios, algo que sería imposible de hacer con métodos tradicionales.
De forma general, el cálculo integral se utiliza para:
- Medir áreas y volúmenes: por ejemplo, el área bajo una curva o el volumen de una figura irregular.
- Analizar el movimiento y la física: calcular distancias recorridas, energías, trabajos realizados o trayectorias.
- Modelar procesos naturales: como el crecimiento de una población, la propagación de una enfermedad o el flujo de un río.
- Resolver problemas económicos: como el cálculo de ingresos acumulados, costos totales o excedentes.
- Interpretar datos continuos: en estadística y probabilidad, las integrales permiten calcular probabilidades en variables continuas.
En resumen, el cálculo integral es una herramienta matemática para pasar de lo infinitamente pequeño a una visión global, y gracias a ello, se convierte en una pieza esencial en casi todas las ciencias y áreas del conocimiento.
Breve Historia del Cálculo Integral
Para comprender mejor qué es el cálculo integral y por qué es tan importante hoy en día, vale la pena mirar un poco hacia atrás en su historia. Aunque solemos asociar el cálculo con Newton y Leibniz en el siglo XVII, sus raíces se remontan a muchos siglos antes.
- Antigüedad: Los primeros intentos de resolver problemas de áreas y volúmenes aparecen en la civilización griega. El matemático Arquímedes utilizaba el llamado método de exhaución, que consistía en dividir figuras en partes cada vez más pequeñas para aproximar su área o volumen. Esta idea es muy similar al principio de las integrales.
- Edad Media: Matemáticos árabes como Alhazen desarrollaron avances importantes en geometría y sumas infinitas, que más tarde servirían de base para los métodos integrales.
- Siglo XVII: Fue aquí donde ocurrió la gran revolución. De manera casi simultánea, Isaac Newton en Inglaterra y Gottfried Wilhelm Leibniz en Alemania desarrollaron de forma independiente el cálculo infinitesimal. Ellos no solo definieron el concepto de integral, sino que también descubrieron su conexión con las derivadas, dando origen al Teorema Fundamental del Cálculo.
- Siglo XIX y XX: Matemáticos como Riemann y Lebesgue formalizaron el concepto de integral, dándole mayor rigor y extendiendo su aplicación más allá de la geometría hacia el análisis moderno, la estadística y la teoría de probabilidades.
Hoy en día, el cálculo integral no solo es una rama de las matemáticas, sino también un lenguaje universal para describir fenómenos continuos en física, economía, biología, ingeniería y prácticamente cualquier ciencia moderna.
El Teorema Fundamental del Cálculo
Para entender a fondo qué es el cálculo integral, es necesario conocer una de sus bases más importantes: el Teorema Fundamental del Cálculo. Este teorema establece la conexión entre las dos grandes ramas del cálculo: la derivación y la integración.
En palabras simples, dice que integrar y derivar son procesos inversos. Gracias a esta relación, podemos calcular integrales de manera práctica utilizando antiderivadas, en lugar de recurrir únicamente a sumas infinitas.
El teorema se resume en dos ideas principales:
- Primera parte del teorema
Si $F(x)$ es una antiderivada de $f(x)$, entonces la integral definida de $f(x)$ entre $a$ y $b$ puede calcularse como: $$
\int_a^b f(x)\,dx = F(b) – F(a)
$$ Esto significa que para encontrar un área bajo la curva basta con evaluar la antiderivada en los extremos. 🔹 Ejemplo: $$
\int_0^2 x^2\,dx = \left[\frac{x^3}{3}\right]_0^2 = \frac{8}{3}
$$ Así obtenemos el área bajo la parábola $f(x) = x^2$ desde $x = 0$ hasta $x = 2$. - Segunda parte del teorema
Si definimos una función a partir de una integral, su derivada recupera la función original: $$
\frac{d}{dx} \left( \int_a^x f(t)\,dt \right) = f(x)
$$ Es decir, derivar lo que hemos acumulado mediante una integral nos devuelve el punto de partida.
¿Por qué es tan importante este teorema?
El Teorema Fundamental del Cálculo nos permite pasar de la teoría a la práctica. Sin él, calcular áreas o volúmenes sería un proceso interminable de sumas infinitas. Gracias a este teorema, hoy en día podemos resolver en minutos problemas que antes parecían imposibles.
En definitiva, este teorema es la pieza que une el cálculo diferencial con el cálculo integral, y es la razón por la cual ambas ramas se estudian juntas dentro del análisis matemático.
Métodos de Integración
Ahora que ya tienes una idea de qué es el cálculo integral y conoces el Teorema Fundamental del Cálculo, es momento de aprender cómo se resuelven las integrales en la práctica. Existen diferentes métodos de integración, y cada uno se aplica según la forma de la función que queremos integrar.
Aquí tienes los principales:
1. Integración directa o por fórmulas básicas
Es el método más sencillo: consiste en aplicar reglas conocidas de integración.
$$
\int x^n\,dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1)
$$
🔹 Ejemplo:
$$
\int 3x^2\,dx = x^3 + C
$$
2. Sustitución
Se usa cuando la integral tiene una función compuesta. La idea es hacer un cambio de variable que simplifique la expresión.
🔹 Ejemplo:
$$
\int 2x \cos(x^2)\,dx
$$
Si tomamos $u = x^2$, entonces $du = 2x\,dx$.
$$
\int 2x \cos(x^2)\,dx =$$
$$=\int \cos(u)\,du = \sin(u) + C$$
$$ = \sin(x^2) + C
$$
3. Integración por partes
Es útil cuando la integral resulta del producto de dos funciones. Está basada en la regla del producto de la derivada:
$$
\int u\,dv = uv – \int v\,du
$$
🔹 Ejemplo:
$$
\int x e^x\,dx
$$
Sea $u = x$ y $dv = e^x dx$. Entonces $du = dx$ y $v = e^x$.
$$
\int x e^x\,dx = x e^x – \int e^x dx = x e^x – e^x + C
$$
4. Fracciones parciales
Se aplica cuando la función es una fracción algebraica. La idea es descomponer la fracción compleja en fracciones más simples que se integran fácilmente.
🔹 Ejemplo:
$$
\int \frac{1}{x^2-1}\,dx
$$
Se descompone como:
$$
\frac{1}{x^2-1} = \frac{1}{2(x-1)} – \frac{1}{2(x+1)}
$$
Entonces:
$$
\int \frac{1}{x^2-1}\,dx $$
$$= \tfrac{1}{2} \ln|x-1| – \tfrac{1}{2} \ln|x+1| + C
$$
5. Integrales trigonométricas y trigonometría inversa
Se utilizan identidades trigonométricas para simplificar integrales que contienen senos, cosenos u otras funciones trigonométricas.
🔹 Ejemplo:
$$
\int \sin^2(x)\,dx = \int \frac{1-\cos(2x)}{2}\,dx$$
$$ = \frac{x}{2} – \frac{\sin(2x)}{4} + C
$$
6. Métodos numéricos
Cuando la integral no se puede resolver de forma exacta, se usan aproximaciones como:
- Regla del trapecio
- Regla de Simpson
Estos métodos dividen el área bajo la curva en figuras simples (rectángulos, trapecios o parábolas) y suman sus áreas para aproximar el resultado.
✅ Los métodos de integración son herramientas que permiten resolver en la práctica lo que significa en teoría qué es el cálculo integral: acumular cantidades infinitamente pequeñas para obtener un valor total.
Aplicaciones del Cálculo Integral
Una vez que comprendes qué es el cálculo integral y sus fundamentos, lo realmente fascinante es descubrir todo lo que puedes hacer con él. El cálculo integral no es solo una herramienta matemática abstracta, sino un recurso esencial para resolver problemas en la vida real y en diferentes disciplinas del conocimiento.
En esencia, el cálculo integral permite modelar, analizar y resolver situaciones donde se requiere acumular, medir o predecir fenómenos que cambian continuamente. A continuación, te mostramos algunas de sus aplicaciones más importantes:
1. Geometría y áreas bajo curvas
Una de las aplicaciones más conocidas es el cálculo de áreas bajo curvas. Por ejemplo, si quieres saber la superficie exacta que hay bajo la gráfica de una función en un intervalo específico, el cálculo integral te da la respuesta precisa. Esto es muy útil en ingeniería, arquitectura y diseño.
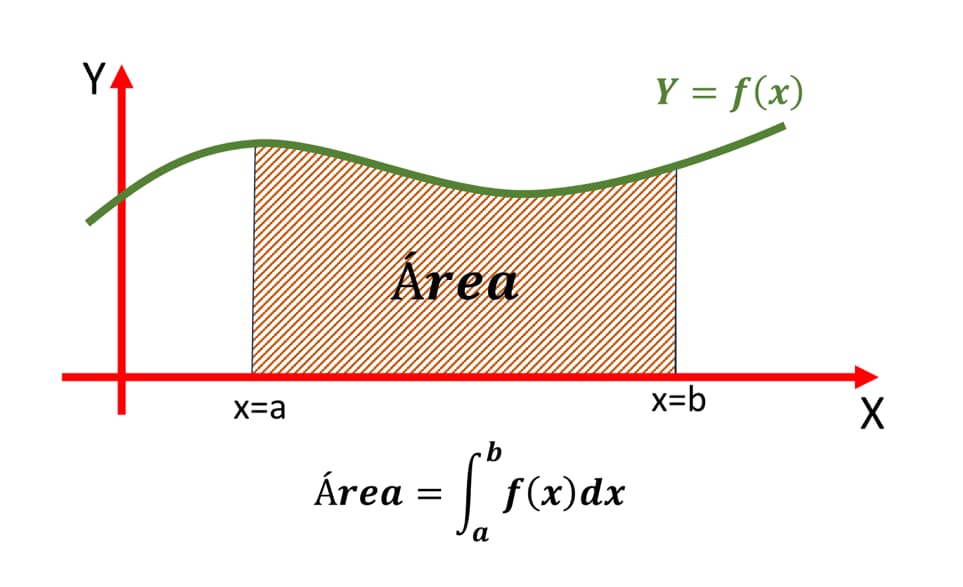
2. Física: movimiento y energía
En física, el cálculo integral ayuda a encontrar magnitudes como:
- Distancia recorrida por un objeto cuando se conoce su velocidad variable.
- Trabajo realizado por una fuerza que cambia en el tiempo o en la posición.
- Energía acumulada en sistemas eléctricos, mecánicos o térmicos.
Sin cálculo integral, muchas leyes de la física modernas serían imposibles de formular.
3. Economía y finanzas
El cálculo integral también tiene aplicaciones en ciencias sociales. Se utiliza para:
- Calcular ingresos totales cuando la tasa de ingresos varía en el tiempo.
- Estimar costos acumulados en procesos de producción.
- Analizar crecimiento poblacional o de mercados, modelando fenómenos dinámicos.
4. Biología y medicina
En biología, el cálculo integral se aplica al estudio de poblaciones, crecimiento de bacterias y transmisión de enfermedades. En medicina, ayuda a modelar la propagación de medicamentos en el cuerpo y calcular dosis precisas en tratamientos.
5. Ingeniería y tecnología
Los ingenieros utilizan el cálculo integral para diseñar estructuras seguras, optimizar sistemas de energía, calcular resistencias de materiales y analizar fluidos en movimiento. También es clave en el desarrollo de algoritmos en inteligencia artificial y procesamiento de señales.
6. Astronomía y ciencias naturales
El cálculo integral permite determinar órbitas de planetas, la trayectoria de cohetes, o la intensidad de la luz y la radiación en el espacio. Sin él, gran parte de los avances en la exploración espacial no serían posibles.
Temas desarrollados de cálculo integral
En esta sección encontrarás una lista organizada de los principales temas relacionados con el cálculo integral. Cada uno está desarrollado de manera clara y progresiva para que puedas avanzar paso a paso en tu aprendizaje, desde los fundamentos hasta las aplicaciones más avanzadas.
¿Qué se necesita para aprender Cálculo Integral?
Para aprender Cálculo Integral, lo primero que necesitas es una mente curiosa y una actitud positiva hacia las matemáticas. No se trata solo de memorizar fórmulas, sino de comprender conceptos profundos que te permitirán resolver problemas complejos. Además, es útil contar con una buena base en álgebra y trigonometría, ya que estos son los bloques de construcción sobre los cuales se asienta el cálculo. ¡Con dedicación y práctica, te sorprenderás de lo que eres capaz de lograr!
¿Qué debo saber para entender Cálculo Integral?
Antes de sumergirte en el Cálculo Integral, es esencial tener un buen dominio del Cálculo Diferencial, especialmente en temas como derivadas y sus aplicaciones. Conocer cómo se comportan las funciones y cómo se representan gráficamente también es muy útil. Esto te ayudará a entender la relación entre derivadas e integrales, un concepto fascinante conocido como el Teorema Fundamental del Cálculo. ¡Una vez que conectes estos conceptos, el mundo del Cálculo Integral se abrirá ante ti como un universo lleno de posibilidades!
Cómo aprender Cálculo Integral
Aprender cálculo integral puede parecer un reto al inicio, pero con la guía adecuada, práctica constante y buenos recursos, cualquiera puede dominarlo. La clave está en avanzar paso a paso, reforzar las bases y apoyarse en materiales confiables que expliquen los conceptos de manera clara y accesible.
Aquí tienes un plan y recursos recomendados para aprender cálculo integral:
1. Reforzar las bases previas
Antes de sumergirte en el cálculo integral, asegúrate de comprender:
- Álgebra básica (ecuaciones, polinomios).
- Funciones y gráficas.
- Cálculo diferencial (derivadas).
Estos conocimientos son esenciales para que el estudio del cálculo integral fluya sin dificultades.
2. Recursos en línea gratuitos
- 📘 Khan Academy – Cálculo Integral: Plataforma gratuita y muy didáctica con videos y ejercicios prácticos.
👉 Visitar Khan Academy - 🎥 YouTube – JulioProfe: Canal educativo en español con explicaciones claras sobre integrales.
👉 Ver canal JulioProfe - 📑 Paul’s Online Notes (en inglés): Notas detalladas con ejemplos paso a paso.
👉 Acceder a Paul’s Notes
3. Cursos completos
- 🎓 Coursera – Cálculo Integral (Universidad Nacional Autónoma de México): Curso en español con teoría y práctica.
👉 Explorar curso en Coursera - 🎓 edX – Calculus 2 (MIT): Curso avanzado en inglés que profundiza en integrales y aplicaciones.
👉 Explorar curso en edX
4. Libros recomendados
- Cálculo de una variable – James Stewart: Un clásico para estudiantes de cálculo, con ejemplos claros.
- Cálculo – Larson y Edwards: Muy utilizado en universidades, con teoría y práctica extensa.
- Cálculo Infinitesimal – Michael Spivak: Ideal para quienes buscan profundidad matemática.
5. Estrategias de estudio
- Resolver ejercicios todos los días, empezando por integrales sencillas.
- Alternar teoría con práctica: leer primero, aplicar después.
- Explicar en voz alta lo aprendido: ayuda a consolidar los conceptos.
- Usar software matemático como WolframAlpha o GeoGebra para visualizar las integrales.
Para aprender cálculo integral necesitas paciencia, práctica y constancia. No importa tu nivel inicial: con buenos recursos, disciplina y el hábito de ejercitarte cada día, podrás dominar el tema y aprovechar todas las aplicaciones que este poderoso campo de las matemáticas ofrece.
Software para Cálculo Integral
- WolframAlpha
- Un motor de conocimiento computacional muy potente. Permite resolver integrales definidas e indefinidas paso a paso.
- 🔗 WolframAlpha
- GeoGebra
- Popular en el ámbito educativo. Permite trabajar con integrales, graficar funciones y visualizar áreas bajo la curva.
- 🔗 GeoGebra
- Mathematica
- Herramienta avanzada de cálculo simbólico y numérico. Muy utilizada en investigación y universidades.
- 🔗 Mathematica
- Maple
- Potente software matemático para cálculo simbólico, con amplia aplicación en ingeniería y ciencia.
- 🔗 Maple
- MATLAB
- Más orientado a cálculo numérico, pero también resuelve integrales simbólicas con su caja de herramientas simbólicas.
- 🔗 MATLAB
- Maxima (gratuito y de código abierto)
- Una alternativa libre que ofrece cálculo simbólico, incluyendo derivadas e integrales.
- 🔗 Maxima
- Integral Calculator
- Calculadora en línea muy práctica para resolver integrales paso a paso.
- 🔗 Integral Calculator
👉 Estos programas no solo sirven para resolver integrales, sino también para aprender, ya que muchos muestran el procedimiento paso a paso y permiten visualizar gráficamente lo que significa integrar.
Conclusión
El cálculo integral es mucho más que una rama de las matemáticas: es una herramienta poderosa para comprender y transformar el mundo que nos rodea. Desde el simple hecho de calcular un área bajo una curva hasta resolver complejos problemas de física, ingeniería o economía, el cálculo integral nos permite acumular lo infinitamente pequeño para explicar fenómenos de gran escala.
Hemos visto qué es el cálculo integral, para qué sirve, sus métodos principales, el Teorema Fundamental y algunas de sus múltiples aplicaciones en la vida real. Además, te compartimos recursos y software especializados para que aprendas y practiques de manera efectiva.
En definitiva, dominar el cálculo integral no solo fortalece tu pensamiento lógico y analítico, sino que también abre las puertas a innumerables campos del conocimiento. Si te comprometes a estudiarlo paso a paso, pronto descubrirás que esta rama de las matemáticas es una aliada esencial para entender mejor la naturaleza, la ciencia y la tecnología.
